
Las matemáticas son una materia compleja y a determinados niveles complicada. La complejidad radica en que tiene varias y muy diferentes vertientes.
Alfonso J. Población || ABC
Por una parte está su carácter técnico (los algoritmos y resultados que nos permiten resolver ejercicios o problemas que se presentan con frecuencia en nuestra vida; lo único de lo que hemos tenido noticia en la etapa escolar y de un modo muy limitado), y por otra su propia concepción y construcción, mucho más próxima a la filosofía que a una ciencia experimental. Aunque predomine una de esas dos facetas, no dejaremos de incluir aquello que nos parezca asequible de ambas, en un intento de que el lector conozca un poco mejor esta disciplina, y descubra que no consiste sólo en “echar cuentas” sin mayor alcance.
Es habitual escuchar la excusa de no entender las matemáticas. Como con todo en esta vida, la dificultad de los niveles es variable, depende de cada persona y de muchos factores, como el interés que uno tenga, cómo y quién nos enseñe, etc.; el menos determinante, aunque no se lo crean, es la capacidad intelectual. Soy de los que piensan que cualquier persona con una inteligencia media normal puede aprender cualquier cosa: unos lo harán en tres segundos, otros en cinco horas y otros en una semana, pero con tesón e interés, se logra. Lo que suele fallarnos es precisamente el interés. Por tanto, ante cualquier texto (de cualquier materia) coexistirán diferentes niveles de lectura y profundización. Cada cual debe quedarse en el que le interese.
Por poner un ejemplo concreto, es habitual encontrar en redes sociales expresiones como la de la imagen, seguidas de alguna expresión de asombro tipo “Magia”, “La belleza de las matemáticas”, u otras similares para calificarlas.
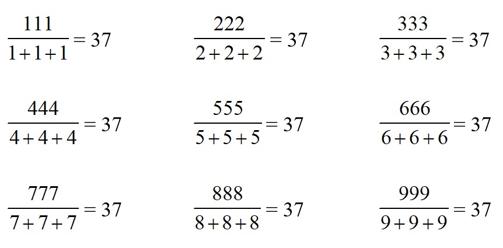
No sé lo que hacen otros compañeros ante imágenes así (que abundan). Sospecho que pasar de ellas esbozando media sonrisa. En mi caso, como mi cabeza cada vez tiene menos hueco libre para aventuras calculistas, eché mano de un papel y un bolígrafo, y garabateé unas cuentas:
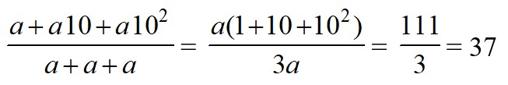
En definitiva, para cualquier dígito a no nulo (si no, no hubiéramos podido simplificar la segunda fracción), el valor siempre es el mismo, no existe magia alguna (como en ninguna otra parte). Respecto a lo de la belleza, es obviamente una apreciación totalmente subjetiva. Más interesante puede ser la cuestión derivada de esta particularidad de los números de tres cifras: ¿existirán igualdades similares para números con otro número de cifras?
Uno puede ponerse a comprobar casos concretos, como hemos hecho en este caso, pero una de las peculiaridades de las matemáticas (y de los matemáticos, por tanto) es que nos gusta saber que pasa siempre, en general, sea cuál sea el número de cifras (por eso demostramos proposiciones, lemas, teoremas, etc.). ¿Se les ocurre cómo podríamos hacerlo en este caso? Es evidente que en el numerador de esas fracciones tenemos un número de n cifras iguales. Esos números podemos representarlos en general con una suma del tipo
![]()
y los denominadores serían de la forma a?n. Observen que n representa el número de cifras. En el caso anterior, n es igual a 3, ya que eran números de tres cifras.
Una forma general de describir ese caso particular sería mediante la expresión
Lee la nota completa en ABC

